Some things make your brain shut off. You just see complex, not looking closer. Big O Notation can be like that. It’s a way to describe the efficiency of an algorithm, how the “speed” is affected by the growth of the input, n. Computing it can be tricky, so start off just learning how to read it.

Here are some simple examples.

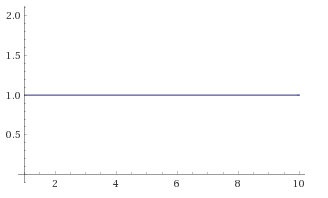
O(1)

const funk = (n) => { }

Constant - It doesn’t matter what the size of n is. This function will always take the same amount of time to run.

Constant

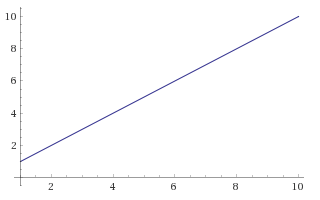
O(n)

const funk = (n) => {
  n.forEach(x => { })
}

Linear - This as the size of n grows, the time to run this function will grow linearly.

Linear

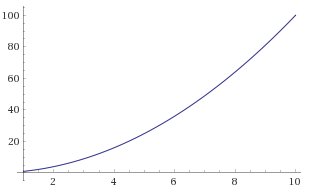
O(n2)

const funk = (n) => {
  n.forEach(x => {
    n.forEach(y => { })
  })
}

Squared - For each item in n we loop, then again within each loop.

Squared

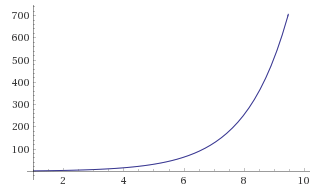
O(2n)

const funk = (n) => {
  return (n <= 1)
    ? n
    : funk(n - 2) + funk(n - 1)
}

Exponential - The time doubles for each increase of n; it grows exponentially. This is OK for small inputs, but will quickly start to suck as n grows.

Exponential

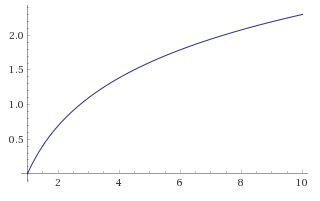
O(log n)

const funk = (n) => {
  return (n <= 1)
    ? n
    : funk(n / 2)
}

Logarithmic - The time for this function grows more slowly as n increases, logarithmically, the inverse of exponential growth. These kind of algorithms cost a lot initially, but pay off for big inputs.

Logarithmic

Nice References